
MHF4U
Culminating Activity
Rates of Change In Career
TRIGONOMETRIC FUNCTION
SINE FUNCTION

COSINE FUNCTION

Both of sine and cosine functions are the sinusoidal function, they are periodic. For sine function, the starting point is zero and goes up to 1 at first, so the rates of change in this period is positive. However, when f(x)=1, the slope is zero. Therefore, the rate of change of the function degrease from one positive number to 0. After that, the valur of f(x) keeps decreasing to -1,the rate of changeis minimum at f(x)=0, so the rates of change decreases until f(x) becomes 0. After that, the slope increases to zero, and then keep increasing until f(x)=0 again. Although the rates of change is not constant, but smoothly, so the line of the function is curved. For cosine function, it is the same meanng as sine(x+π/2), so the rates of change decreases from zero. the rates of change of this function is same process from the second step of sine function.
COSECANT FUNCTION

SECANT FUNCTION

Both of the cosicant and secant function have rate of change of zero when f(x)=1, -1, and then right side of f(x)=1, both rates of change is decreasing. On the other hands , the left side of it, the rates of change starts increasing. For f(x)=-1, rates of change is increasing to zero at right side. At left side, the rates of change is decreasing from 0 to negative number. This relationship fits for both of cosecant and secant functions because we can rewrite secant function as csc(x+π/2).
In this way, the rates of change is not constant, but the change of it is smooth. Therefore, the line of the function is curved.
Meteorology
TANGENT FUNCTION
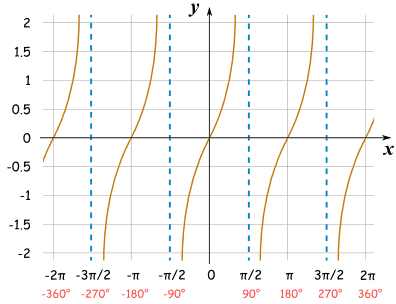
The rate of change of the tangent function is always positive, so the line of the function goes from bottom to up. This function depends on the sine and cosine values since tanx=(sinx/cosx). Therefore, the tangent function is also periodic function. When the sinx=0, the tanx=0,and then whe cosx=0, tanx=undefined since the denominator is zero.
When the cosx becomes zero, the sinx is still increasing, so the rates of change is larger than sinx=0. Therefore, the function's slope is smaller near tanx=0
COTANGENT FUNCTION

The cotangent function is also periodic since cotx=cosx/sinx. At this time, when the cosx=0, cotx=0, and then when sinx=0, cotx=undefined since the denominator is sinx. Also, the rates of change in entire graph are negative, so the graph goes from the positive to negative infinity. Furthermore, sinx=cos(x-π/2), so the graph translate in π/2 to th left. When sinx=0, the cosx is bigger than other situation, so the slopeof the function near cosx=0 is a little bit smaller than others.
APPLICATION QUESTIONS

The meteorologist is the career researching the weather conditions and then forecast accurate datas for us. They ususally observe the cloud motion and color and shape of them because if the weather is worse, the speed of cloud gets more and more fast.Furthermore, the black cloud leads thunsars, and the cloud which causes heavy rain is called Cumulonimbus, and then its shape is like the steep mountain. Also, they try to estimate the temperature using the change of air pressure in the world, and then announce the weather condition to be calm down. The things related to trigonometric function in this career is the temperature change in a year. The temperature in the same seasons are almost same each year. Also, the temperature has one cycle and then repeats almost same cycle every yesr. Therefore, the trigonometric function is related in the change of the temperature.

The Town of Geogia is relatively warm in the world. The temperature in this town is represented by the function: y=4sin[2π/365(x-80)]+14. Determine the instantaneous rate of change at x=87.
1. straegy of using interval
Units of the symbols: x=days, y=degrees in Celcius
